Wykres skrzynkowy, pudełkowy, ramka – wąsy lub z angielskiego box plot.
Wiele nazw a wykres ten sam. My będziemy nazywali go wykresem skrzynkowym. Nie wiem czy nazwa ta jest najbardziej popularna czy nie. Na pewno jesteśmy do niej najbardziej przywiązani i to właśnie jej używamy w naszej codziennej pracy. W dzisiejszym poście chcemy omówić każdy element wykresu skrzynkowego, a jak się za chwilę okaże, jest on dosyć rozbudowany. Niesie on ze sobą wiele informacji, więc dobrze jest zrozumieć co przedstawiają.
Po co rysujemy wykres i dlaczego akurat skrzynkowe? Niczego nowego przed Tobą nie odkryjemy ponieważ często inne rodzaje wykresów rysuje się w tym samym celu. Wykresy skrzynkowe rysujemy zazwyczaj z dwóch powodów.
- Eksploracja danych
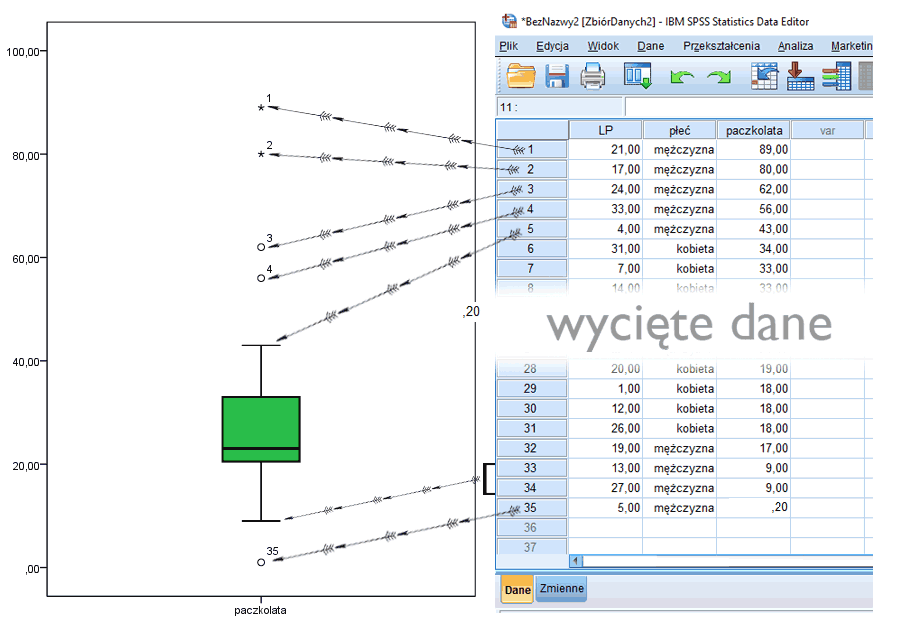
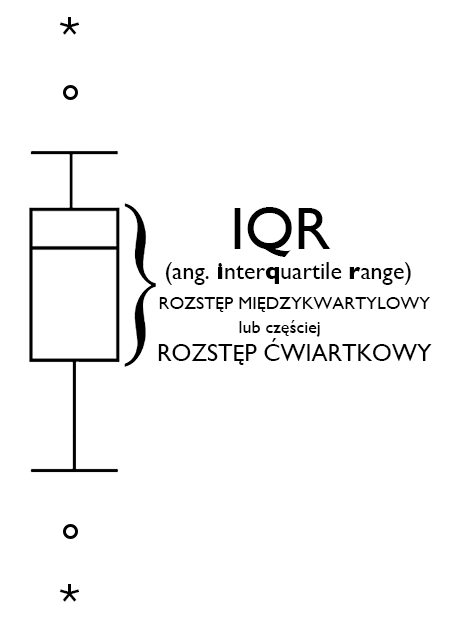
Z uwagi na wartość informacyjną wykresów skrzynkowych są one często wykorzystywane w pierwszym lub drugim kroku stosunkowo pobieżnej eksploracji danych, z którymi przyjdzie zmierzyć się analitykowi. Bez potrzeby przeglądania, czasami gigantycznych tabel z podstawowymi statystykami opisowymi, klikania tu, klikania tam, wystarczy szybki rzut oka na wykres by zobaczyć “co w trawie piszczy”. Prawdopodobnie najważniejszy jest jednak fakt, że wykresy skrzynkowe wskazują na to czy w bazie danych występują obserwacje odstające czy nie. Wynik nietypowy, odstający od reszty, outlier czy nawet dewiant to nazwa obserwacji (najczęściej wyniku badanej osoby lub innego podmiotu badań), której rezultat może negatywnie wpłynąć na wyniki przeprowadzanych testów statystycznych. Dobrze jest mieć narzędzie, które jest detektorem takich przypadków (choć wykres skrzynkowy nie jest jedyny)
- Zilustrowanie różnic między grupami lub między kolejnymi pomiarami
Szczególnie w przypadku analiz statystycznych w naukach medycznych zdarza nam się ilustrować różnice między porównywanymi grupami lub kolejnymi pomiarami wykonanymi w różnych odstępach czasu, przy użyciu wykresu skrzynkowego. W medycynie, biotechnologii i im podobnych bardzo często wykonuje się po prostu testy nieparametryczne w celu potwierdzenia postawionych hipotez. Gdy wykonujemy testy nieparametryczne, które nie porównują przecież średnich arytmetycznych tylko inne miary, dobrze jest wykonać właśnie wykresy skrzynkowe zamiast standardowych wykresów słupkowych lub innych prezentujących średnie i przedziały ufności, odchylenia lub błędy standardowe. Wykresy skrzynkowe prezentują mediany i odchylenia od nich, a to bardzo dobry sposób ilustracji wyników uzyskanych w toku przeprowadzonych testów nieparametrycznych.