Korelacja
Po co wykonujemy badanie korelacyjne?
Analiza korelacji w statystyce polega na zbadaniu czy dwie zmienne są ze sobą istotnie statystycznie powiązane. Innymi słowy, sprawdza czy jakiekolwiek dwie cechy, atrybuty lub własności (wyrażone liczbowo) współwystępują ze sobą. Obliczany współczynnik zawsze waha się od -1 do 1.
Bardzo ważne w analizie korelacji jest to, że nie bada ona związku przyczynowo-skutkowego a po prostu związek/współwystępowanie dwóch zmiennych. Gdy badamy czy dwie zmienne są skorelowane ze sobą to nie wiemy, która zmienna wpływa na którą. Wiemy tylko, że wartość jednej zmiennej rośnie/maleje w przypadku wzrostu/spadku wartości drugiej zmiennej. Nie wiemy jednak czy to spadek/wzrost zmiennej A wpływa na zmianę wartości w zakresie zmiennej B czy spadek/wzrost wartości zmiennej B wpływa na zmiany wartości w zakresie zmiennej A.
Przeprowadzając analizę korelacji interpretujemy:
1. czy związek występuje – czy jest istotny statystycznie
2. jaki jest znak współczynnika korelacji – ujemny czy dodatni, mówimy o korelacji negatywnej lub pozytywnej (korelacja ujemna/negatywna
3. jak silny jest to związek ( przyjmuje się, że wartości korelacji od 0 do 0,3 oznaczają słaby związek, od 0,3 do 0,5 związek umiarkowanie silny natomiast wartości od 0,5 do 1 mówi o związku silnym lub bardzo silnym)
- Wyniki analizy korelacji graficznie prezentuje się na tak zwanym wykresie rozrzutu, który zamieszczamy poniżej w ramach opisywanego przykładu.
- Najczęściej stosowane współczynniki korelacji to r Pearsona, rho Spearmana oraz tau b Kendalla.
PRZYKŁAD: Wyobraźmy sobie, że chcemy sprawdzić czy istnieje związek pomiędzy latami nauki szkolnej a poziomem samooceny wyrażonym na skali od 0 do 100. Wyliczony współczynnik korelacji r Pearsona (wynik korelacji) wynosi r = 0,79; p < 0,001. Oznacza to, że zachodzi istotna statystycznie korelacja pomiędzy dwiema zmiennymi. Jest to związek silny (ponieważ jest z przedziału 0,5-1) oraz dodatni (ponieważ przed współczynnikiem nie ma minusa). Dodatni znak korelacji mówi o tym, że wraz ze wzrostem lat nauki szkolnej wzrasta poziom samooceny. Na etapie nauki statystyki warto jest również napisać w przykładowym raporcie, że wraz ze wzrostem samooceny rośnie również liczba lat nauki szkolnej. Pokażecie tym samym, że jesteście świadomi braku informacji o związku przyczynowo-skutkowym. Nie wiemy czy to lata nauki szkolnej wpływają na samoocenę czy może samoocena wpływa na to, że więcej lat się edukujemy. Poniższy wykres jest prezentacją graficzną opisanego związku.
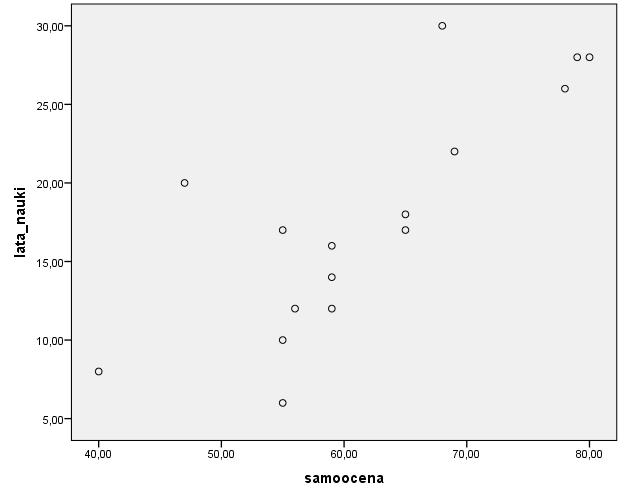
Badania korelacyjne często sprawiają trudność osobom, które nigdy wcześniej nie miały kontaktu z matematyką stosowaną lub choćby podstawami statystyki na swojej uczelni. Wystarczy jednak odpowiedni plan i wytyczne, aby móc się z nimi uporać a następnie poprawnie przeanalizować zebrane dane.
Polecam w tym miejscu dwa ciekawe wpisy o tym, że współczynniki korelacji czasami potrafią płatać figle – które wcale nie są figlami a “normalnymi” wynikami 🙂
CZĘŚĆ 1 – https://pogotowiestatystyczne.pl/analizy-statystyczne-bez-tajemnic-czyli-dziwne-wyniki-analizy-korelacji-podziale-podzbiory-cz-1/






